Impossible chessboard puzzle

2021/11/21, ermouth

I took the problem from a nice Standup Math channel video, however my initial way of thinking was very different from the proposed solution. Much more cumbersome and complex, I admit.

Anyway, there’s a lot of interesting nuances in the problem to make it worth writing this post.

Initial thoughts

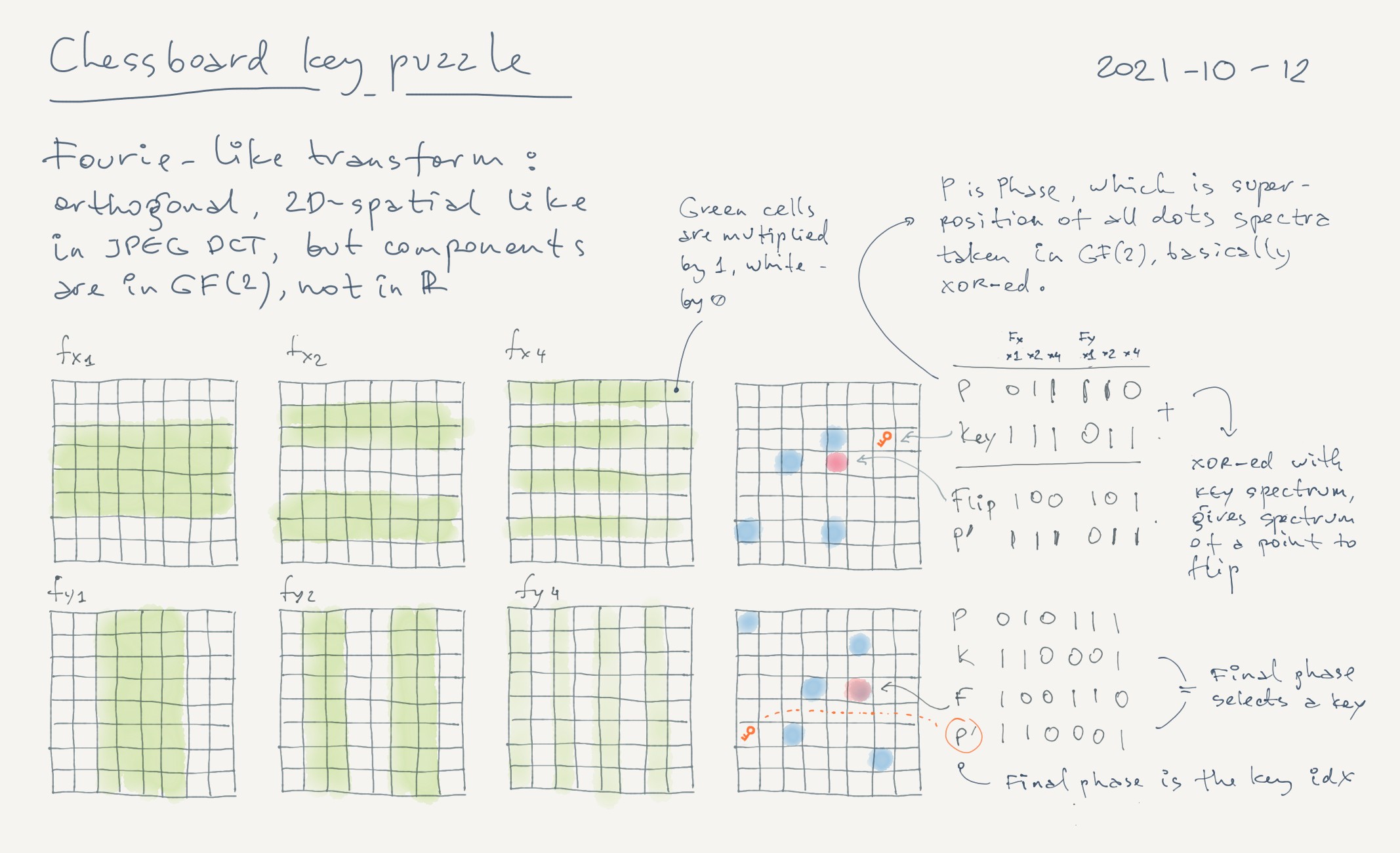
Each board cell is encoded with a 6-bit index, so to point on a certain cell any 64-bit state of the board must somehow be collapsed into 6 bit. 

First of all, 6 digits suggest we must choose orthonormal basis with 6 dimensions. Then we somehow project the board state on each axis, and then fold each respective value into 1 bit. 

We then somehow mix K, a 6-bit index of the key position taken in our basis, with W, 6-bit state of the board. It must yield F: 6 bit index pointing on a coin to flip. After the coin is flipped, a newly emerged board state X should become equal to K.

Let’s denote a flip of the coin at F over state W as +. 

So W+F == K, also since X+F == W, and X == K, we seemingly have a contradiction, K–W == K+W, which looks like it cannot be always true. However, nothing wrong with this if we choose such a construct where addition operation is indistinguishable from subtraction, at least for for 1-bit numbers because we add/subtract for each digit independently.

There exist one suitable, GF(2). In GF(2) addition is equivalent to subtraction, and this combined operation is better known as XOR.

Choosing a basis

The first idea which came into mind was pretty bizarre, but to my surprise it immediately solved the puzzle. Several decades ago I spent a lot of time trying to understand how JPEG works, and was amazed with spectra magic. I clearly remember spectra-like structures are additive, produce orthonormal basis, and from much later reading I also remember there exist Fourier-like transforms over GF(2ⁿ). Latter turned out to be completely unrelated, but anyway...

So we can try to do a trick somewhat like JPEG DCT transform does: we obtain 6 bits as a 2D spatial DCT-like transform, with only 3 frequencies horizontally and 3 vertically. This trick is supposed to give us a vector of 6 real numbers, which we must then convert into vector of six 1-bit numbers.

To make conversion more transparent we replace cosine with meander, and take parity as a result. Btw if we perform amplitude summation in GF(2) right from the beginning, we end up with exactly parity. 

Interactive example below implements the transform. Each of 6 green squares is a mask, only dark green cells are accounted. Each mask is laid over board and the parity of heads count is taken as a result for the respective bit. 

The cell with the blue round dot ● has exactly same ‘spectrum’ as current board state entirely. We can say that the board state is pointing to a cell with the dot.

Note the chosen basis is rotation-safe only when number of heads is odd like in example above. ‘Rotation-safe’ here means the dot moves along with rotations.

If we change number of heads to even (click any cell), the dot starts toggling between only 2 positions instead of 4 possible rotations, or stays completely fixed regardless of rotation.

Also note there exists a cell with the coin that doesn’t change W when flipped. For above basis that cell is the bottom right corner. Any possible valid basis has such a cell with 000000 ‘spectrum’.

Another approach

The basis above (6 green squares) is not unique, there are other bases, and also approaches to find them. From later thinking it became obvious that spectrum approach is dramatically over-complicated, however valid.

We can do much simpler.

Imagine we start counting heads parity by quadrants 4×4, so we need 2 bits to point to a particular quadrant. Then we count heads parity for each quadrant 2×2 in larger quadrant, we need another 2 bits, and then we count inside that small quadrants, another 2 bits. 

The basis generated in this way, with bits taken in proper order, is pretty remarkable: W is a dotted cell’s index in binary, if counted from left-top. Also the basis has striking similarities with previous one, but seems less symmetric, which will be helpful later. 

Anyway, rotations behave the same: ok for odd number of heads and tails, but fail to keep relative position of the dot for even number of heads. Below example isn’t rotation-proof, it has even number of heads.

Further I gonna use this particular basis in most cases, it’s elegant and much more concise than DCT-derived.

Putting a key

A cell with the key has its own 6-bit ‘spectrum’ K, which can be obtained if we apply our masks and count bits over a board with only one coin at the key’s position. XOR-ing W with K, we get an index of the coin to flip. Below widget makes the process interactive. 

The cell F to flip is marked red, clicking it puts the dot over the key, which means current board state points to the key’s cell. Also you can right-click any cell to move the key into it.

Different bases obviously yield different results, so prisoners must select a particular basis upfront.

What about rotations?

The problem description tells us we have a chessboard. Unlike ordinary 8×8 grid, a chessboard has 2 colors, or have A…H and 1…8 marks, or both. So if we have marks we know exactly where the top-left corner is – which guarantees positive outcome. 

But what if there were no marks and we had just a checkerboard?

Checkers, not chess

Checkerboard complicates both guess process and rules. P1 and P2 can only agree on a diagonal: say, they agree to choose a rotation where top left cell is white. 

For initial states with even number of heads all 90º rotations are no different. So if P2 sees odd number of heads he can always decide where the key is.

But what if we started off with odd number of heads? Any flip makes number of both heads and tails even which produces seemingly undecidable state. 

However P1 and P2 still can agree how to decide which end of diagonal they choose. To calculate the rotation we can again use agreed basis but in a different way: we compare number of heads in each half of each basis axis as after we already flipped a coin.

We take one green square of selected basis, and then count heads for both light and dark green cells. We count in regular decimal, and then compare. 

There can be 3 outcomes: more heads at light side, more at dark, or they are equal. Let’s agree if there’s more on light side we choose that side as containing top left corner, and stop. If there’s more on dark side, we rotate board 180º and stop. If they are equal we take next digit.

Below widget has ∆’ field, which shows result of such comparison. Easy to see 180º rotation turns all < chars into > and vice versa, so we can choose a valid corner to start from.

But does this trick always work?

Undecidable symmetries

If P2 sees a state which is self-symmetric over both x and y, or up to 90º rotation, or up to 180º rotation, he still can’t decide. 

The only way to get into those states is to have the key in 0-th position. We may account key in the cell #63 as #0 because they are equivalent up to rotation.

Easy to see all those cases, after normalizing key to 0-th position, has W==0 after coin flip. So we have 1/64×1/64=1/4096 chance to have initial state which is undecidable for checkerboards. Probably we can somehow select asymmetric basis to solve those cases.

Anyway, for chessboards with known top left corner, a8, prisoners can always solve the puzzle.

Other bases and solutions

There can be a large variety of bases, both looking symmetric and asymmetric: 

Also YouTube is full of different solutions, most interesting is about 6 dimensional cube rotations:

Also there exists good related publication at Cantor’s Paradise, which shows several other approaches.